机器学习

本文从连续时间随机微分方程的角度介绍扩散模型。

1. 维纳过程（Wiener Process） 和 布朗运动（Brownian Motion）

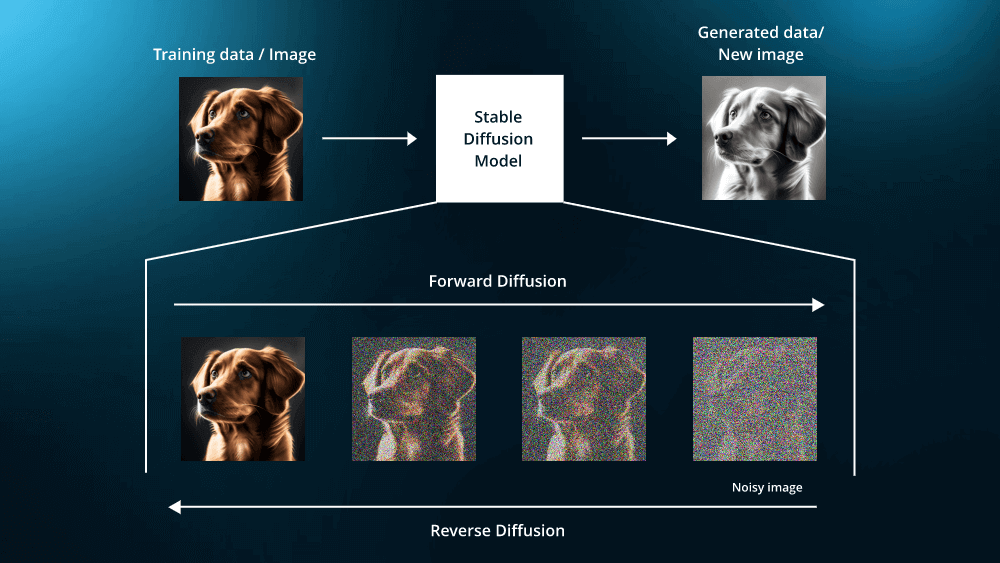
如果从连续时间角度看，扩散模型的加噪过程实际上就是在扩散的常微分方程基础上增加了一个布朗运动漂移的过程
布朗运动/维纳过程 WtW_t 需要满足以下性质：

  1. W0=0W_0=0
  2. 独立增量：

P(Wt+u−Wt)=P(Wt+u−Wt∣Wt)\begin{align} P\left( W_{t+u}-W_t \right) =P\left( W_{t+u}-W_t|W_t \right) \end{align}

  1. 增量满足正态分布 ：

(Wt+u−Wt)∼N(0,u)\begin{align} \left( W_{t+u}-W_t \right) \sim \mathcal{N} \left( 0,u \right) \end{align}

  1. WtW_t 随时间tt几乎一定连续 (almost surely)。

有了布朗运动的性质，为了后面证明需要需要用到下面三条引理：

  1. 噪声微元的分布：

dWtdWt=dtεdtε=dtε2,where  ε∼N(0,1)\begin{align} dW_tdW_t=\sqrt{dt}\varepsilon \sqrt{dt}\varepsilon =dt\varepsilon ^2, where\,\,\varepsilon \sim \mathcal{N} \left( 0,1 \right) \end{align}

  1. 噪声微元的二阶原点矩等于时间微元， 方差则是时间微元的无穷小量

E[dWtdWt]=dt    D[dWtdWt]  ∝  dtdt≡o(dt)\begin{align} E\left[ dW_tdW_t \right] =dt\,\,\,\, D\left[ dW_tdW_t \right] \,\,\propto \,\,dtdt\equiv o\left( dt \right) \end{align}

  1. 由第二条引理可以推出一下性质几乎一定满足（因为期望是定值，方差满足无穷小量）：

dWtdWt=dt\begin{align} dW_tdW_t=dt \end{align}