机器学习

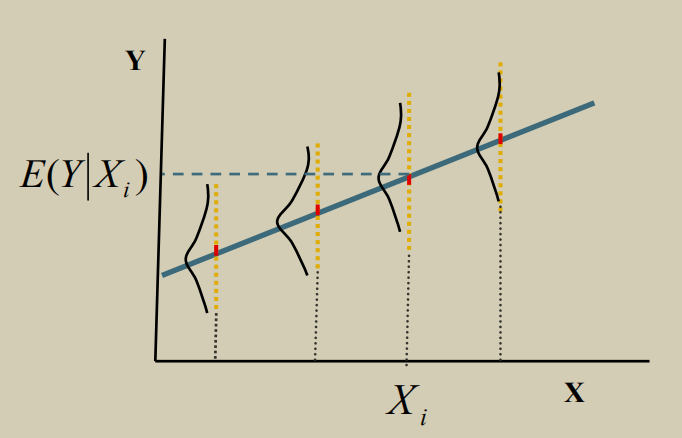
给定一系列样本点，找到贯穿样本点的直线; 处理这个问题有两类方法，一种是线性回归，另一种是主成分分析。本文从优化目标来比较两者区别。

由于两类方法比较经典，教程也较多，本文不再详细介绍二类方法。

假定样本点为：

(x^1,y^1),(x^2,y^2),…,(x^N,y^N)\begin{align} \left( \hat{x}_1,\hat{y}_1 \right) ,\left( \hat{x}_2,\hat{y}_2 \right) ,\dots ,\left( \hat{x}_N,\hat{y}_N \right) \end{align}

1. 线性回归

线性回归假设直线方程为: y=kx+by=kx+b, 众所周知它的优化目标是尽可能减小预测yiy_i以及真值 y^i\hat{y}_i之间的距离的平方：

min⁡∑i=1N(yi−y^i)2⇒min⁡k,b∑i=1N(kxi+b−y^i)2\begin{align} \min \sum_{i=1}^N{\left( y_i-\hat{y}_i \right) ^2}\Rightarrow \underset{k,b}{\min}\sum_{i=1}^N{\left( kx_i+b-\hat{y}_i \right) ^2} \end{align}

上式就是我们熟知的最小二乘法。对kk和bb分别求偏导并令偏导为0即可求解出最终的k^\hat{k}和b^\hat{b}。推导过程和最终结果省略。

2. 主成分分析

与线性回归不同，主成分分析的优化目标是最小化点到直线距离，假设直线方程为ax+by+c=0ax+by+c=0。 简单起见，如果假设样本点均值和最终的直线截距均为0, 则直线方程简化为 ax+by=0ax+by=0.

从解析几何的性质可知：假设某个样本点坐标为

(x^i,y^i)\begin{align} \left( \hat{x}_i,\hat{y}_i \right) \end{align}

那么这个样本点到直线距离如下：

di=ax^i+by^ia2+b2\begin{align} d_i=\frac{a\hat{x}_i+b\hat{y}_i}{\sqrt{a^2+b^2}} \end{align}

最终优化目标可以表示为最小化所有点到直线的距离平方和：

min⁡∑i=1Ndi2\begin{align} \min \sum_{i=1}^N{d_{i}^{2}} \end{align}

如果把优化参数写成列向量的形式 w≡(a;b)∈R2×1\boldsymbol{w}\equiv\left(a;b\right) \in \mathbb{R}^{2\times1} 数据点写成行向量的形式 pi≡(x^i,y^i)∈R1×2\boldsymbol{p}_i\equiv\left(\hat{x}_i,\hat{y}_i\right) \in \mathbb{R}^{1\times2},那么公式(4)可以写成如下表达：

di=piw∥w∥2\begin{align} d_i=\frac{\boldsymbol{p}_i\boldsymbol{w}}{\left\| \boldsymbol{w}\right\|_2} \end{align}

如果约束 ∥w∥2=1\left\| \boldsymbol{w}\right\| _2=1，并且所有点集合用大矩阵 P≡(p1;p2;… ;pN)∈Rn×2\boldsymbol{P}\equiv \left( \boldsymbol{p}_1;\boldsymbol{p}_2;\dots ;\boldsymbol{p}_N \right) \in \mathbb{R}^{n\times2}表示，那么优化目标(5)可以转化为：

min⁡w∑i=1N(piw)2,  s.t. ∥w∥2=1⇒min⁡w  wTPTPw,  s.t. wTw=1\begin{align} \underset{\boldsymbol{w}}{\min}\sum_{i=1}^N{\left( \boldsymbol{p}_i\boldsymbol{w} \right) ^2 },\,\, s.t. \,\left\| \boldsymbol{w} \right\| _2=1 \\ \Rightarrow \underset{\boldsymbol{w}}{\min}\,\,\boldsymbol{w}^T\boldsymbol{P}^T\boldsymbol{Pw},\,\, s.t.\, \boldsymbol{w}^T\boldsymbol{w}=1 \end{align}

上式可以使用拉格朗日乘子法求解：

wTPTPw+λwTw\begin{align} \boldsymbol{w}^T\boldsymbol{P}^T\boldsymbol{Pw}+\lambda \boldsymbol{w}^T\boldsymbol{w} \end{align}

对 w\boldsymbol{w}求偏导并令导数为零：

2PTPw+2λw=0⇒PTPw=(−λ)w\begin{align} 2\boldsymbol{P}^T\boldsymbol{Pw}+2\lambda \boldsymbol{w}=0 \\ \Rightarrow \boldsymbol{P}^T\boldsymbol{Pw}=\left( -\lambda \right) \boldsymbol{w} \end{align}

问题转化为对协方差矩阵（零均值假设）PTP∈R2×2\boldsymbol{P}^T\boldsymbol{P} \in \mathbb{R}^{2\times 2}求特征值和特征向量。下面分析拉格朗日乘子λ\lambda的物理意义，由于2阶方阵最多有两个特征值，那么应该选取哪个特征值呢？ 特征值有如下性质推导：

∑i=1Ndi2=wTPTPw=(−λ)wT(−λ)w=λ2wTw=λ2\begin{align} \sum_{i=1}^N{d_{i}^{2}}&=\boldsymbol{w}^T\boldsymbol{P}^T\boldsymbol{Pw} \\ &=\left( -\lambda \right) \boldsymbol{w}^T\left( -\lambda \right) \boldsymbol{w} \\ &=\lambda ^2\boldsymbol{w}^T\boldsymbol{w}=\lambda^2 \end{align}

可知，优化目标值就是特征值的平方，由于我们希望优化目标值越小越好，因此选择绝对值较小的特征值对应的特征向量作为最终的解。

特点总结：

  • 线性回归通常用于两变量相关性分析以及机器学习预测， 它的侧重点是变量分析和预测本身, 数据点的坐标分量物理意义明确。但是优化目标和结果高度依赖坐标轴的选取和建立。
  • 主成分分析直接建模点到直线的距离，它不依赖坐标系的选取，优化结果具有旋转、镜像等变性。适合几何建模。